Inf9 1.5 Relative und absolute Adressierung

Zu den Au fgaben

Wirklich sinnvoll sind Tabellenkalkulationssysteme in dem Moment, wenn man viele Daten auf einmal auswertet. So ist es nicht unüblich, wenn Tabellen Hunderte von Zeilen mit Berechnungen enthalten. Unser bisheriges Vorgehen, jede Zeile einzeln zu bearbeiten, ist in so einer Anwendung nicht praktikabel. Daher bietet das Tabellenkalkulationssystem verschiedene Abkürzungen.

1.5.1 Funktionsbereiche

In vielen Funktionen, die eine variable Anzahl von Eingabewerten haben können, kann man, statt die Zellen einzeln anzugeben, einen Funktionsbereich festlegen. Die Zellen werden in diesem Fall nicht mehr mit einem ; sondern einem : angegeben.

Um Funktionsbereiche anzugeben, gibt man Anfang und Ende des Funktionsbereiches an. Das Trennzeichen ist dabei : statt dem üblichen ;.
Merksatz 1.5.1.1

Vorher	Nachher
`=SUMME(A1;A2;A3;A4;A5)`	`=SUMME(A1:A5)`
`=SUMME(A1;B1;C1;D1;E1)`	`=SUMME(A1:E1)`
`=ANZAHL(A1;A2;...;A150)`	`=SUMME(A1:A150)`

Beispiele für die Abkürzungen durch Funktionsbereiche

1.5.2 Adressierung

Möchte man in zwei aufeinanderfolgenden Zeilen oder Spalten die gleiche Berechnung durchführen, kann man die Zeile „herunterziehen“. Dabei klickt man den kleinen schwarzen Kasten in der unteren rechten Ecke einer markierten Zelle und zieht ihn bei gehaltener Maustaste in die gewünschte Richtung.

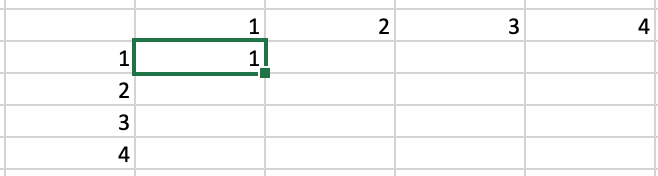
Beim ziehen nach rechts/links werden alle Adressen innerhalb unserer Formel an die neue Spalte angepasst. Analog verändert das Ziehen nach oben/unten die Zeilennummer. Da die Adressen zur jeweiligen Zelle relativ betrachtet gleich bleiben, nennen wir diese Art der Adressierung die relative Adressierung.
Merksatz 1.5.2.1

Bei manchen Formeln möchte man, dass beim Ziehen der Formel eine Zellen Spalte oder Zeile nicht verändert wird. Damit dies möglich ist, muss man markieren, ob die Zeile oder Spalte festgehalten werden soll.

Um beim kopieren von Formeln die Zeilennummer oder den Spaltenbuchstaben festzuhalten stellt man ein $ Zeichen davor. Da die absolute Bezeichnung der Zelle, die referenziert wird, somit nicht verändert werden kann, spricht man von absoluter Adressierung.
Merksatz 1.5.2.2

Zelleninhalt	Auswirkung
`C$5`	Nummer ändert sich nicht beim Ziehen nach oben/unten
`$D4`	Buchstabe ändert sich nicht beim Ziehen nach rechts/links
`$E$8`	Zellenbezeichnung ändert sich nie, egal in welche Richtung gezogen wird.

Beispiele für Anwendung des $ Operators

Aufgabe 1:

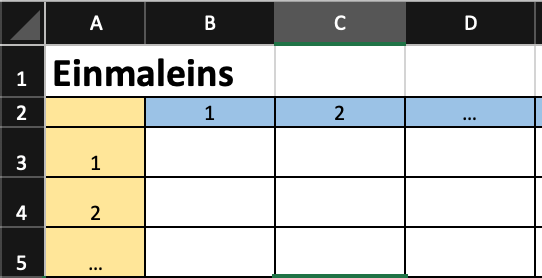
Erstelle ein Rechenblatt, in dem das Einmaleins bis 15 mal 15 ausgerechnet wird.

Aufgabe 2:

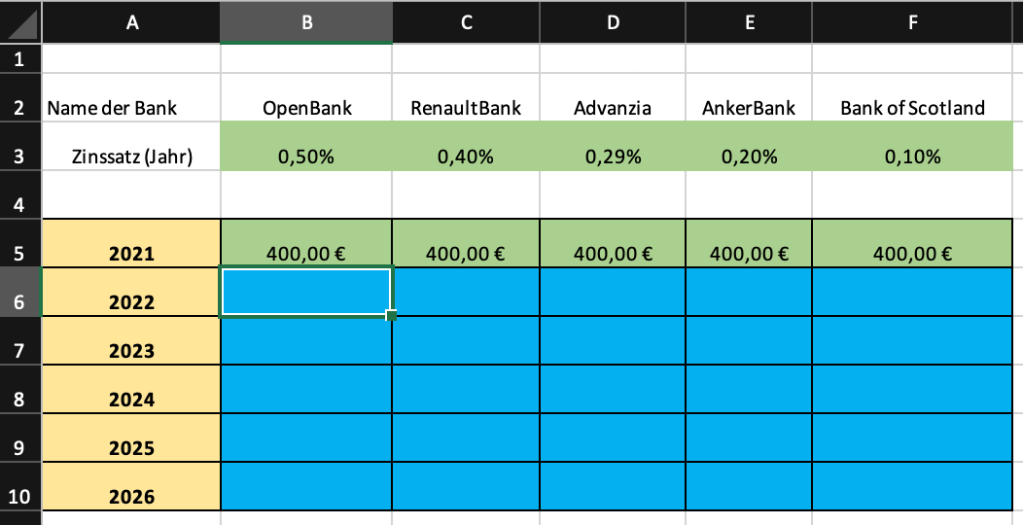
Erstelle ein Rechenblatt, nach dem Schema rechts. Vervollständige die Jahre 2022 bis 2026 so, dass man immer den Kontostand beim gegebenen Zinssatz bekommt.

Aufgabe 3:

Ein Elektrofachhändler gibt am Black Friday Rabatt auf seine Produkte. Erstelle ein Rechenblatt, das den Rabatt nach Waren ausrechnet. Dabei sollte man den Rabatt oben immer dynamisch anpassen können.

Aufgabe 4:

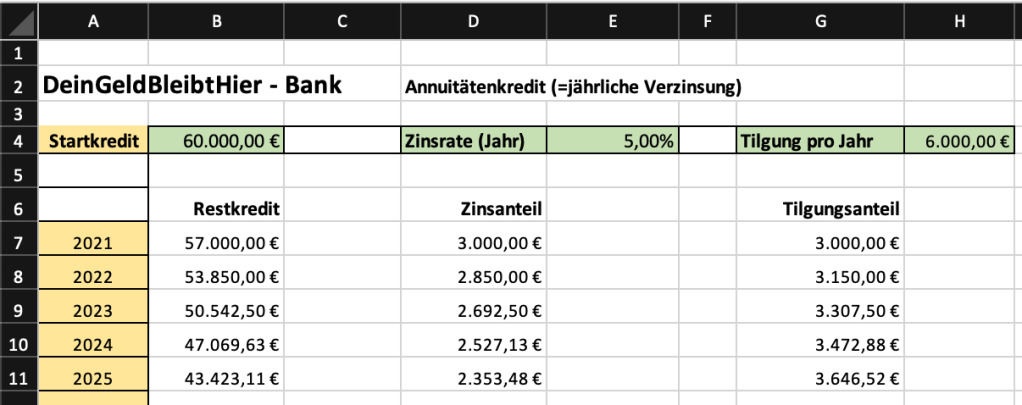
Ein Annuitätenkredit wird oft zur Finanzierung von Krediten verwendet. Das besondere an diesem Kredit ist, dass man jährlich gleich viel abbezahlt. Der Betrag der Anzahlung besteht jedoch aus Zinsen und Tilgung. Nur die Tilgung reduziert die Schulden.

Der Zinsanteil berechnet sich dabei indem man den Kreditbetrag mit dem Zinssatz multipliziert. Die Tilgung entspricht dem gezahlten Betrag pro Jahr abzüglich den Zinsen.

Erstelle ein Rechenblatt, in dem man oben die Kreditsumme, Kreditzinssatz und jährliche Abzahlung einträgt und untern die Übersicht über Restschulden, Zinsen und Tilgung, am Beispiel eines 60 000€ Kredites mit 5% Zinsen und 6000€ Kreditabzahlung pro Jahr, sieht. Teste dein Rechenblatt dann mit einem realistischen Münchner Hauskredit: Recherchiere dafür die aktuelle Kreditzinsen und den Preis eines Einfamilienhauses in deinem Wohnort.