In unserer hochtechnischen Welt sind es schon lange nicht mehr nur die Computer, die Aufgaben für uns Menschen übernehmen. In jedem Gerät, das Strom braucht, steck irgendwo eine Platine, auf der Programme Aufgaben unseres Alltages für uns erledigen. Dabei müssen beim Schreiben von effizienten Algorithmen für solche beschränkten Systeme viele verschiedene Parameter beachtet werden:
- Technische Limits (Speicher, Rechengeschwindigkeit, Platz,…)
- Code-Lesbarkeit und Wartbarkeit (Medizinische Anwendungen, App Stores, Sicherheitssoftware, …)
- Akzeptierte Laufzeit (Finden eines Weges im Navi vs. Training einer KI)
Bisher haben wir uns hauptsächlich Algorithmen angeschaut, die mit den Grundbausteinen aufgebaut werden (Wiederholung, Bedingte Anweisung, Sequenz). Es gibt bei manchen Problemstellungen jedoch eine weitere Art von Algorithmus, die manchmal leichter lesbar/einfacher oder echt schneller in der Berechnung ist.
Das Prinzip der Rekursion besteht darin, dass die Methode für einen Grundwert direkt mit einem Ergebnis abbricht (Abbruchsbedingung) und alle weiteren Werte auf einen einfacheren Fall zurückführt, der uns näher an den Grundwert bringt.
Beispiel: Berechnung der Fakultät
Die Iterative (mit Wiederholung gelöste) Methode der Berechnung einer Fakultät könnte so aussehen:
public long fakultaetIterativ(long n){
long y = 1;
for(int i = 1;i<=n;i=i+1)
{
y = y*i;
}
return y;
}Hier wird in jedem Schritt der Wiederholung der Wert der Variable y mit der Laufvariable i multipliziert. Somit berechnet sie 1*1*2*...*n = n!
Um dies Rekursiv zu lösen braucht man folgenden Code:
public long fakultaetRekursiv(int n) {
if(n == 0 || n == 1){
return 1;
}
return n * fakultaetRekursiv(n - 1);
}Wir sehen in diesem Code, dass die Werte von 0 und 1 als 1 zurückgegeben werden, und alle anderen Fälle auf n*(n-1)! reduziert werden. Wir sehen rechts das Sequenzdiagramm der Methodenaufrufe.
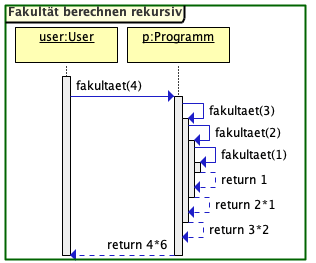
Dabei wird letztendlich die Rekursion mathematisch wie folgt aufgelöst:4! = 4*3! = 4*3*2! = 4*3*2*1! = 4*3*2*1
Welche Algorithmen sind besser?
Die rekursiven Algorithmen brauchen mehr Methodenaufrufe, die im Computer im sogenannten Heap Speicher abgelegt werden. Dafür brauchen manche Algorithmen in einer iterativen Implementierung eine zusätzliche Speicherstruktur für die Zwischenergebnisse. Somit haben beide Arten einen Algorithmus zu schreiben ihre Vor- und Nachteile.
Die Lesbarkeit und der Umfang des Codes variiert teilweise enorm und so muss im Einzelfall entschieden werden, welche Implementierung für ein gegebenes System besser ist.
Theoretisch betrachtet kann man jeden Algorithmus von der einen in die andere Form umschreiben. Es gibt wenige Algorithmen, bei denen dies nicht mit dem Umschreiben von Rekursion in eine Wiederholung mit fester Anzahl möglich ist.
Die Ackermann Funktion ist ein Beispiel in der theoretischen Informatik, das genutzt wird, um zu zeigen, dass nicht alle LOOP (Wiederholung mit Anzahl) berechenbaren Funktionen auch WHILE (Wiederholung mit Bedingung) berechenbar ist.
Aufgaben:
Aufgabe 1:
Programmieren Sie eine rekursive Methode, die die Summe der ersten n Zahlen berechnet.
Aufgabe 2:
Programmieren Sie ein Programm zur Berechnung der n. Fibonacci-Zahl. Erstellen Sie jeweils eine Methode die es iterativ und rekursiv löst.
Die Fibonacci Zahlen sind wie rechts angegeben definiert.
F(1) = 1
F(2) = 1
F(n) = F(n-1) + F(n-2)Hinweis: rekursiv ist leichter
Aufgabe 3:
Erstellen Sie eine Fibonacci Methode, die ein Array mit allen Fibonacci Zahlen bist zum eingegebenen Parameterwert ausgibt. (Rekursiv und Iterativ)
Aufgabe 4:
Schreiben Sie eine rekursive Implementierung der Ackermannfunktion.
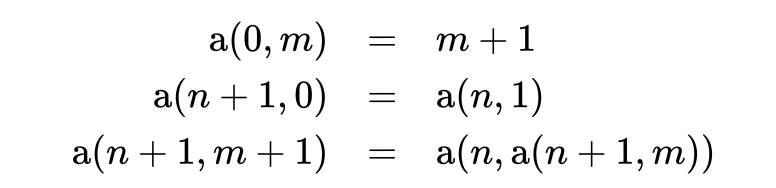
Nach oben
