In vielen Anwendungen müssen wir alle Elemente in einem Graphen durchlaufen. Um uns einen Algorithmus zu überlegen, der alle KNOTEN besucht, betrachten wir ein Anwendungsbeispiel:
Anton, Bert, Carlos, Dominik, Elias, Franz und Georg sind zusammen in einem Wahlkurs an der Schule. Um Informationen untereinander zu verbreiten, schicken Sie sich gegenseitig Nachrichten. Dabei wollen Sie ein Schneeballsystem verwenden, in dem jeder die informiert, deren Nummer er hat, da nicht jeder allen anderen seine Handynummer geben möchte.
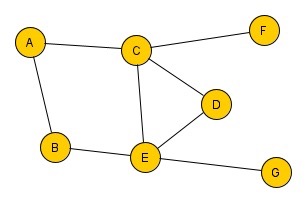
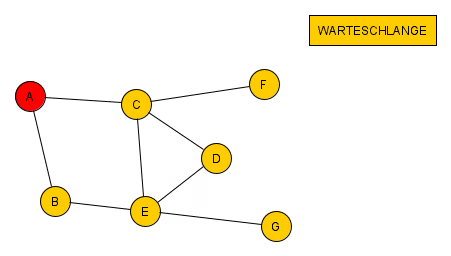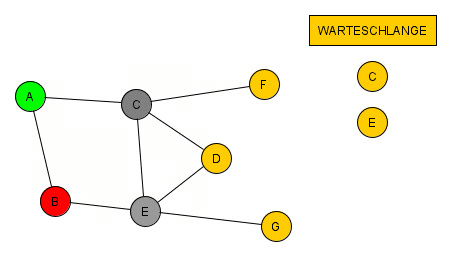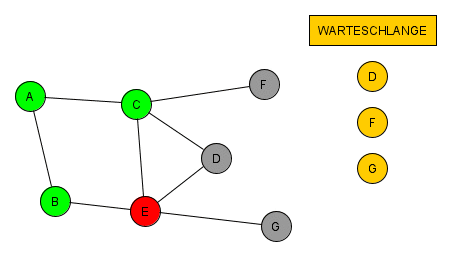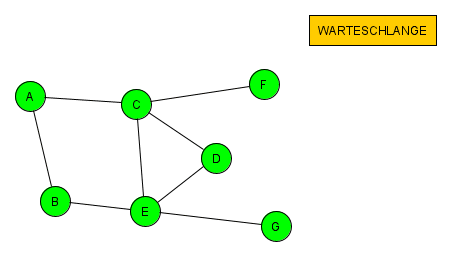
Betrachtet man dieses Problem mit einem Graph, stellen die Knoten die einzelnen Personen und die Kanten jeweils wer wen anschreiben kann. Der Graph könnte dabei zum Beispiel so wie rechts aussehen.
Ziel ist also wieder, dass alle Knoten durchlaufen werden (hier: jeder bekommt die Information). Es ist dabei sinnvoll, ein Feld vorzubereiten, in dem wir speichern, welche erledigt sind.
Angenommen wir beginnen beim Knoten Anton (A). Er müsste nun B und C anrufen und die Information weitergeben, da diese noch nicht besucht wurden.
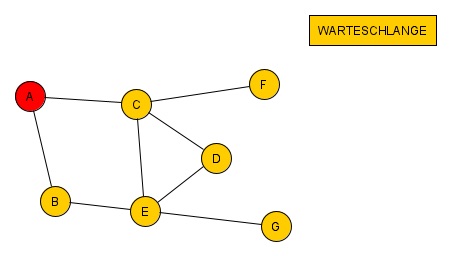
Es erscheint wieder sinnvoll, einfach der Reihe nach vorzugehen und zuerst B und dann C anzurufen.Die beiden werden in dieser Reihenfolge weiterarbeiten und somit in dieser Reihenfolge in die Warteschlange eingefügt.
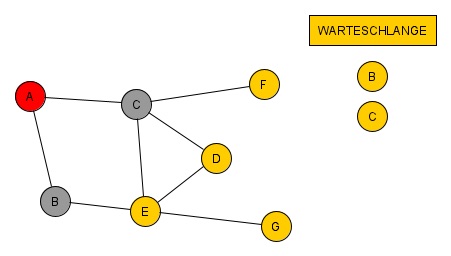
Wir arbeiten weiter und gehen zu Knoten B. Dieser muss wieder überlegen, wer seine Nachbarn sind und diese in die Warteschlange einfügen.
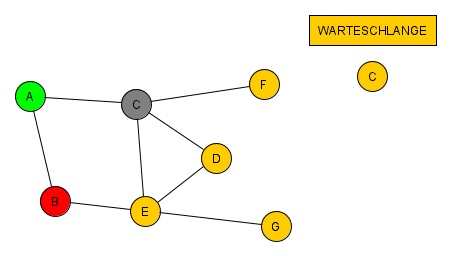
Diesmal ist nur E dazu gekommen. Wir können den Knoten B also abschließen und in der Reihenfolge der Warteschlange weiter machen. Das Prinzip setzt sich fort und wie man unten sieht, geht es immer gleich weiter.

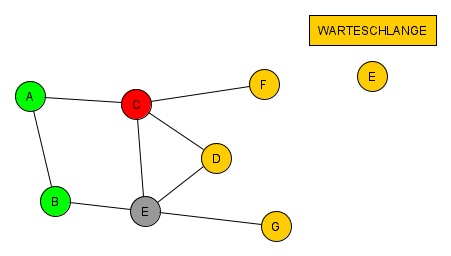
(5. Schritt)
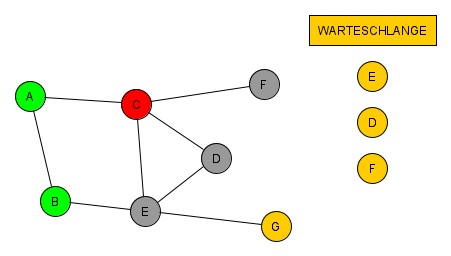
(7. Schritt)
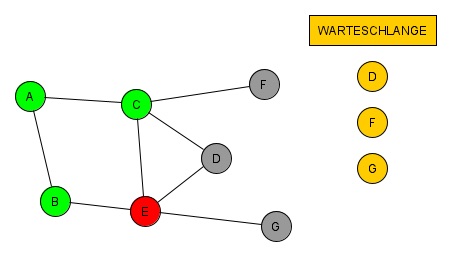
(9. Klasse)
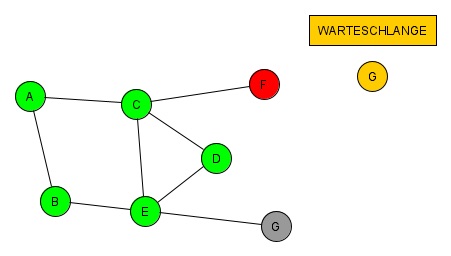
(11. Schritt)
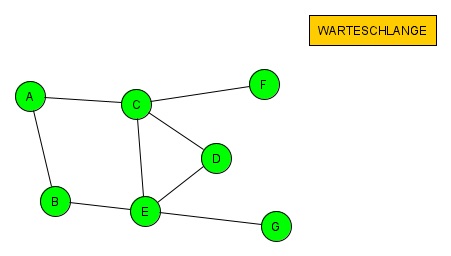
(13. Schritt)

(6. Schritt)
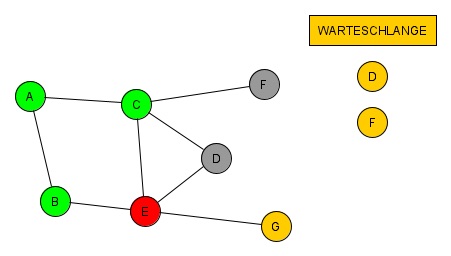
(8. Schritt)
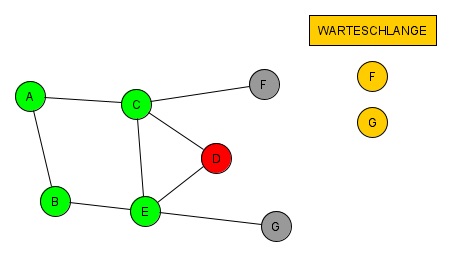
(10. Klasse)
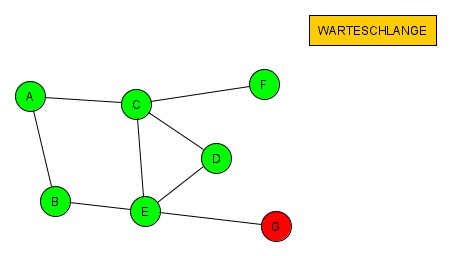
(12. Schritt)
Der Algorithmus läuft also folgendermaßen:
- Besuche den Startknoten
- Speichere alle nicht erledigten Nachbarn in einer Warteschlange (falls sie noch nicht drin sind)
- Markiere aktiven Knoten als erledigt
- Prüfe, ob Warteschlange leer ist.
- Falls Nein: Setze obersten Knoten der Warteschlange als aktiven Knoten und mache bei 2 weiter.
- Falls Ja: Fertig
Die Breitensuche besucht prinzipiell erst alle Nachbarn, bevor man tiefer in den Graph einsteigt. Dabei wird in jedem Knoten immer wieder die gleiche Methode aufgerufen. Wir nennen dieses Prinzip rekursiv.
Merksatz 1.4.1
Umsetzung in Java
Klar ist, dass wir für die Markierungen, welcher Knoten bereits besucht wurde ein Feld mit Datentyp boolean brauchen. Da boolean ein primitiver Datentyp ist, müssen wir im Konstruktor nur angeben, wie groß das Feld ist, da primitive Datentypen automatisch mit einem Wert belegt werden. Bei boolean ist das tatsächlich der Wert false, was uns entgegenkommt.
Das Besuchen an sich können wir wieder mit einer Methode Besuchen lösen, da wir wieder wie bei der Tiefensuche immer wieder das gleiche tun. Wir erinnern uns, dass beim Graph die Adjazenzmatrix und alle Knoten in der Klasse GRAPH vorliegen und wir daher nur in dieser Klasse eine Methode einbauen müssen.
Überlegen wir uns die nötigen Struktogramme der Methoden Breitensuche(int start) und BesucheBFS(int knotenIndex):
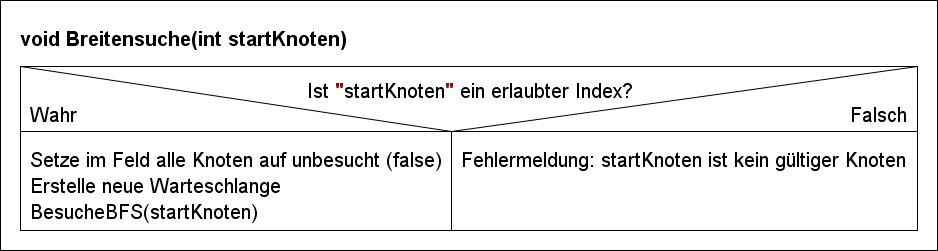
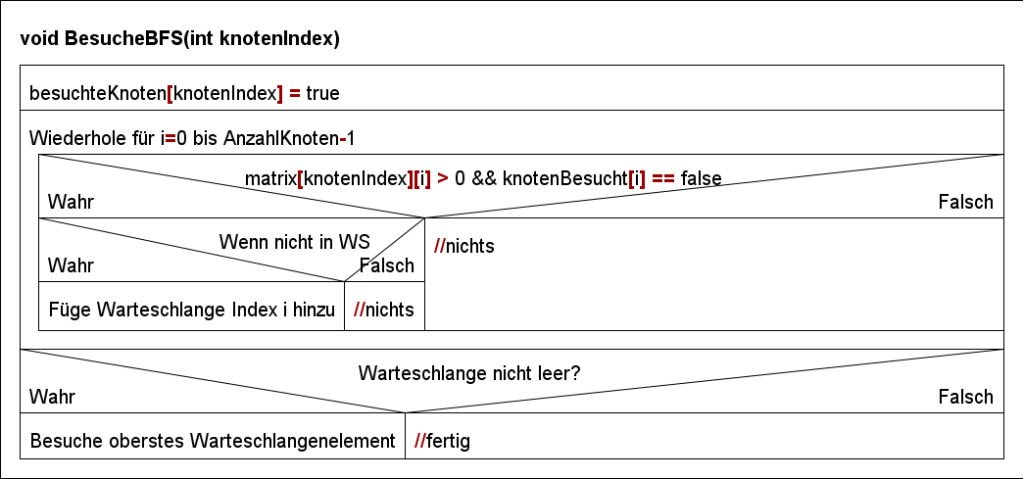
Aufgabe 1:
Überlegen Sie, in welcher Reihenfolge die Knoten im Graphen unten besucht werden würden, wenn man den Graph ausgehend von Knoten 1 nach dem BFS Algorithmus besuchen würde.
Aufgabe 2:
Können Sie einen Graph angeben, in dem man mit dem BFS nicht alle Knoten besuchen würde?
Aufgabe 3:
Machen Sie sich mit der Methode Breitensuche und der Klasse WARTESCHLANGE vertraut. Überlegen Sie vor allem, mit welchen Methoden sie Elemente in die WARTESCHLANGE einfügen und entfernen können und wie man überprüft, ob die WARTESCHLANGE leer ist. Die Vorlage hat diese Methode, die Klasse und das Feld boolean[] erledigt bereits implementiert.
Aufgabe 4:
Implementieren Sie den Algorithmus BFS. Verwenden Sie die Methoden Breitensuche und BesuchenBFS.
Aufgabe 5:
In manchen Anwendungen ist es wichtig, einen „Rahmen-GRAPH“ zu erstellen, der aus dem GRAPH besteht, der nur durch das besuchen nach BFS entsteht. Er enthält alle KNOTEN, aber nur die KANTEN, die beim BFS benutzt wurde. Implementieren Sie eine Methode BFSGraph in der Klasse GRAPH, die aus dem existierenden Graph den Rahmen-GRAPH erstellt und diesen zurückgibt.
