In der Informatik geht es oft darum, reale Probleme mit dem Computer entweder zu lösen, oder wenigstens das Finden einer Lösung zu vereinfachen. Ein alltägliches Problem ist dabei den Weg zu einem unbekannten Ort/einer Straße zu finden. Wir müssen also die Daten von Straßen, Orten und Adressen für den Computer lesbar machen im Hinblick auf die Wegfindung.
Wenn wir einen Straßenplan anschauen, sehen wir, dass viele Informationen überflüssig sind. Dazu gehören unter anderem die Häuser oder sonstige Anlagen. Für den Computer können wir uns also auf folgende Informationen beschränken:
- Straßenverbindungen (mit Einbahnstraßen markiert)
- Orte an die man gehen kann
Damit sieht das Straßenbild in der Innenstadt z.B. vereinfacht so aus:
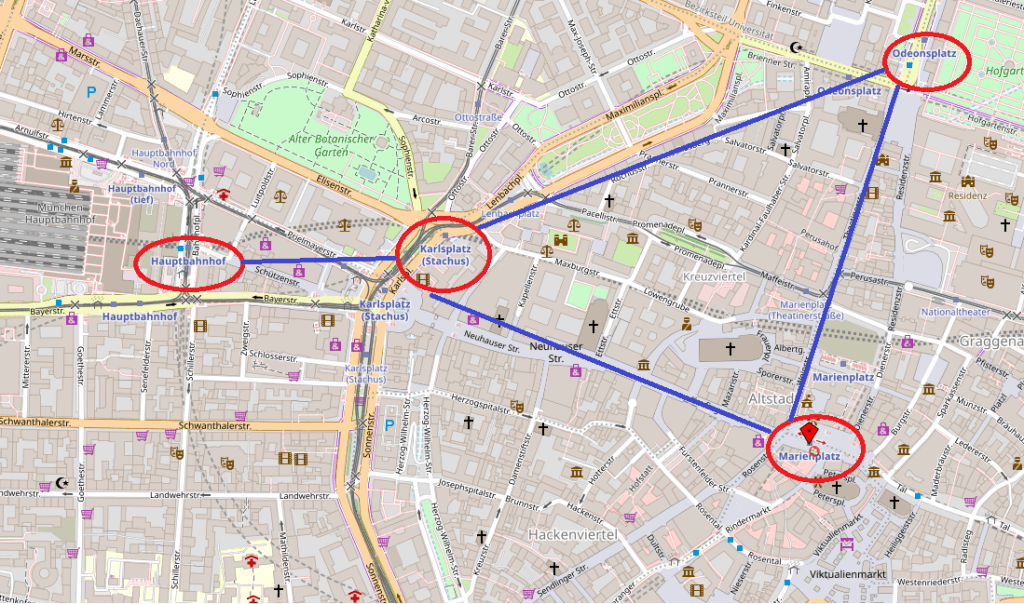
Wenn man nun also alle „unwichtigen“ Details weglässt, nennen wir das entstehende „Diagramm“ einen GRAPH.
Ein Graph besteht aus Knoten und Kanten, welche die Knoten miteinander verbinden. Im Beispiel der Straßennetzes stehen so die Knoten für Orte und Kanten für die verbindenden Straßen.
Merksatz 1.1.1
Grundbegriffe
Um Graphen zu beschreiben verwenden wir folgende Begriffe und Eigenschaften:
| Begriff | Erklärung |
|---|---|
| gerichtet | Die Kanten des Graphen haben nur eine Richtung in der sie durchlaufen werden können. Man stellt dies mit einem Pfeil dar. |
| gewichtet | Die Kanten des Graphen haben als Zusatzinformation eine Gewichtung (Zahl). Dies kann z.B. im Straßennetz die Länge der Straße sein. |
| Pfad | Ein Pfad ist eine Abfolge von Knoten, die immer jeweils mit einer Kante verbunden sein müssen. |
| Zyklus | Ein Pfad, bei dem Anfang und Ende der gleiche Knoten sind. |
| erreichbar | Man nennt einen Knoten erreichbar von einem anderen Knoten, wenn es einen Pfad vom ersten zum zweiten Knoten gibt. |
| zusammenhängend | Man nennt einen Graphen zusammenhängend, wenn jeder knoten von jedem Knoten erreichbar ist. Dabei unterscheidet man zwischen stark (auch mit gerichteten Kanten ist alles erreichbar) und schwach (nur wenn man alle Kanten als ungerichtete betrachtet ist alles erreichbar) zusammenhängend. |
| vollständig | Ein vollständiger Graph hat von jedem Knoten eine Kante zu jedem anderen Knoten. |
Aufgabe 1:
Informieren Sie sich im Internet über die Flugrouten der
Lufthansa. Betrachten Sie die internationalen Flugverbindungen und die nationalen zwischen den Abflugorten ins Ausland.
- Erstellen Sie einen ungewichteten, ungerichteten Graphen für die Flugrouten. Als Knotenbezeichner verwenden Sie die international gebräuchlichen Abkürzungen. Stellen Sie den Graph in einem Zeichenprogramm (z.B. y-Ed) dar.
- Ergänzen Sie den Graphen aus a) zu einem gewichteten Graphen, der die Flugdauer angibt.
- Warum ist der ungerichtete gewichtete Graph für die Flugrouten ungeeignet? Was ist die Ursache für die unterschiedlichen Flugzeiten? Arbeiten Sie in den Graphen aus b) die Unterschiede für einige Kanten ein, bei denen Hin- und Rückflugzeiten sich um mehr als fünf Minuten unterscheiden.
Aufgabe 2:
Das Königsberger Brückenproblem ist eine mathematische Fragestellung aus dem frühen 18.Jahrhundert, die man wie folgt veranschaulichen kann.
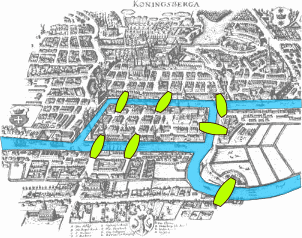
In der Stadt Königsberg gibt es mehrere Inseln, die durch Flüsse getrennt sind. Über die Flüsse führen Brücken. Kann man einen Spaziergang so gestalten, dass man alle Brücken nur genau einmal überquert?
- Veranschaulichen Sie die Fragestellung mit einem Graph.
- Wie würde die Frage nach dem Spaziergang im Graph lauten und was ist die Antwort. Begründen Sie ihr Ergebnis.
Aufgabe 3:
Betrachten Sie folgende Graphen. Welche Graphen sind äquivalent zueinander?